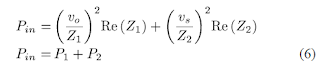Electric Springs- Part 2

OPERATIONS AND LIMITATIONS OF ELECTRIC SPRINGS

For a load that can be divided into two parts: a noncritical load and a critical load , as in Fig. 4. By connecting an electric spring in series with the noncritical load, we can ensure that the voltage and power at the critical load to remain constant when the line voltage feeding the load fluctuates. Such an arrangement of load will be called “smart load.” The aim of the electric spring in the application example of Fig. 4 is to restore to the nominal value of the mains voltage at the location of the device installation. Let be the dynamically-changing input power. The general power balance equation for the system in Fig. 4 is

where and are the root-mean-square values of the noncritical load voltage and the ac mains voltage, respectively; is the real part of that represents the resistive element is the impedance of the “noncritical” load and is the impedance of the “critical” load. The vector equation for the electric spring is

Equation (6) shows that, if the mains voltage is regulated by the electric spring at the nominal value, the second power term should remain constant for the critical load. If the power generated cannot meet the full power for both and, the input-voltage control of the electric spring will generate a voltage vector to keep regulated at . From (7), the voltage vector across will be reduced and so the power consumption of will also be reduced. Therefore, if the electric spring performs well, for the critical load should remain constant as expected and for the noncritical load should follow the power generation profile.

Fig. 3.1.1. Operating modes of the electric spring to maintain to for a noncritical load comprising resistive inductive load. (a) Neutral (b) Inductive mode (noncritical load power reduction for voltage boosting) (c) Capacitive mode (noncritical load power boosting for voltage reduction).

This explanation becomes obvious if Z₁ and Z₂ are considered as pure resistive loads R₁ and R₂  respectively. The scalar (6) will become

If v_s is kept constant by the electric spring, the only variable on the right-hand side of (8) is the electric spring voltage . Critical load power is a constant. The variation of will reduce so that the sum of and will follow the profile of . In other word, the electric spring allows the load power consumption to automatically follow the power generation—which is the new control paradigm required by future power systems with substantial intermittent renewable energy sources .

Like a mechanical spring which cannot be extended beyond a certain displacement, electric spring also has its operating limits. Fig. 6(a)–6(c) shows the vector diagrams of the system (Fig. 4) with the electric spring under three operating modes for a noncritical load comprising an inductive-resistive load (e.g., a lighting load). The circle in the vector diagram represents the nominal value of the mains voltage (e.g., 220 V). The vectors are assumed to rotate in an anticlockwise direction at the mains frequency (e.g., 50 Hz). Fig. 6(a) depicts the situation when the electric spring is in a “neutral” position in which. This refers to the situation that the power generated by the renewable power source (such as a wind farm) is sufficient to meet the load demand and simultaneously maintain at the nominal value of . Fig. 6(b) represents the situation when power reduction in is needed in order to keep v_s at v_{s_ref}  . Here v_a  is positive (making v_o less than v_{s_ref}  ) in order to provide the “power reduction” function under the inductive mode of the electric spring.

Fig. 3.1.2 Schematic of an electric power system with an electric spring connected

in series with a dissipative electric load Z₁.

            If the generated power is higher than the load demand ,v_s will exceed v_{s_ref} , resulting in an over-voltage situation. In order to regulate v_s at v_{s_ref} Fig. 6(c) shows that the electric spring can provide “power boosting” function by operating under the capacitive mode. Here v_o is increased, with respect to its value in Fig. 6(b), in order that the load Z₁ can consume more power generated by the renewable energy source to keep the power balance. The scalar equation for electric spring voltage vector v_a under the capacitive mode [Fig. 6(b)] and inductive mode [Fig. 6(c)] is given in (9).

 

Fig.4.3.2   Operating modes of the electric spring to maintain v_s to v_{s_ref} for a resistive noncritical load in a power system with source impedance of a network box. (a) Neutral v_a =0 . (b) Capacitive mode. (c) Inductive mode.

In a power system context, analysis of the electric spring can be carried out for other types of noncritical loads such as a water heater (i.e., a resistive load). Fig. 7 shows a modified experimental setup in a power system including the source impedance of the power supply and power cable. Due to the presence of the impedance of the network box, the voltage at the generator side is labelled as V_G and the mains voltage at which the electric spring is located is labelled as V_s . The operating modes are illustrated in Fig. 8(a)–8(c). It has been demonstrated in Fig. 4 that a smart load, when operated in a stand-alone mode, maintains constant voltage and power for the critical part of the load .When a smart load is connected to a power distribution system as in the case of Fig. 7, interactions between the system impedance and the smart load, as well as the voltage and power characteristics of the power supply, will affect the performance of the smart load. Due to the injection of both real and reactive power from distributed power sources in future smart grid, the electric springs can be operated dynamically under neutral, capacitive or inductive mode with the objective of regulating the mains voltage